在做航线相关决策时，我们需要参考市场需求和份额的预测结果，QSI模型和MNL模型是被广泛应用的重要工具。航线网络规划第二期，我们聊一聊QSI和MNL的历史由来、构建及应用。

       01  引言

       上期我们介绍了，航线网络规划旨在通过增减航线、调整航线频率、调整时刻等措施，提升航空公司的收益。具体可点击以下链接阅读：航线网络规划（一）：概览

       此外，随着市场份额的提高，规模经济效应使得航空公司对市场的控制能力及管理效率得到提升，其收益将进一步提高。因此，提升或者维护市场份额，也是航线网络规划的重要目标。

       实际上，航空公司在预估收益的时候，往往分为两步：1）预测总体市场需求，即预测“蛋糕”有多大；2）预测可以获得的市场份额，即预测可以分到多少“蛋糕”。因此，在做航线网络规划时，航空公司经常会考虑相关决策对市场份额的影响。而市场份额可以进一步细分到各个航线市场（也被称之为O&D市场），每个航线市场都有很多可选的行程。行程可以由一段或者多段航节组成，一般情况下，单航节的行程可称为直达航班，而由两段或以上的航节组成的行程则被称之为联程航班。这些行程在该航线市场中都存在着竞争关系，如下图所示。

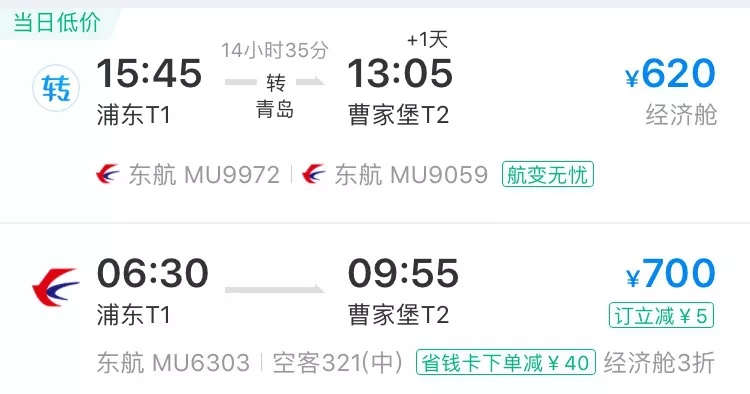
上海-西宁的可选行程     图源：ctrip.com

       航空领域常用的市场份额预测方法有：服务质量指数（quality of service index，QSI）模型、离散选择模型（discrete choice model，DCM）、航班频率“S 曲线”市场份额模型。航班频率“S曲线”在上期已经介绍过，本期将详细介绍QSI和DCM中的的多项Logit模型（Multi-nominal Logit，MNL）。

       02  QSI模型

       历史

       QSI是一种根据多个指标来预测、估算市场份额的指标体系，也是用于预估航线市场份额的代表性方法。QSI由波音公司运筹实验室开发，其认为对某一个航线市场，决定某一航空公司市场份额的主要因素为该航空公司提供的航班质量和飞机有效载量等。QSI模型方法是一种通用性较强的预估方法，尤其适合在较为不熟悉的航线市场上运用。目前世界上先进的航空公司例如荷兰航空（KL）、美国航空（AA）、达美航空（DL）等都会利用自己的市场数据，建立起符合自身实际情况的QSI体系，用以辅助航线决策。

       模型

       如上所述，我们利用QSI衡量旅客对隶属于同一个航线市场的不同行程的偏好。这可以被粗略理解为对同市场的每个行程进行打分。

       既然是“打分”，就涉及旅客在选择行程时所关心的要素，例如承运的航空公司、是否直飞、所需飞行时长、机票价格和执飞的机型等等。

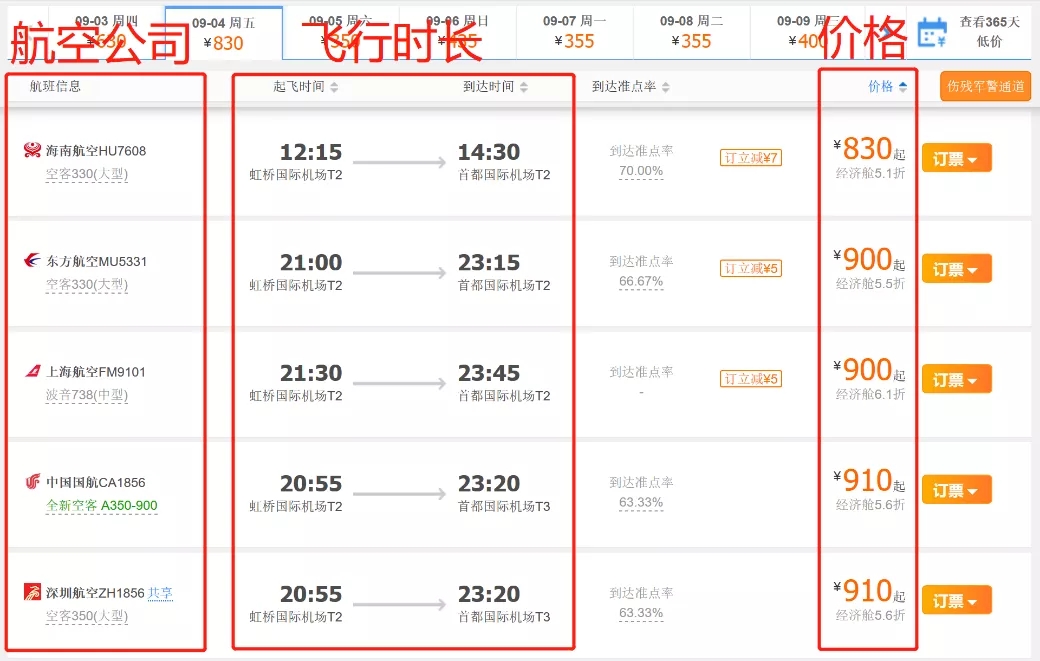
购票平台展示旅客所关心的要素     图源：ctrip.com

       假设，针对行程i，我们考虑4个要素（service characteristic），记作X1，X2，X3，X4，那么我们可以用（包括但不限于）以下形式表示QSI模型：

       1  线性

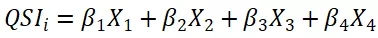
       2  乘积

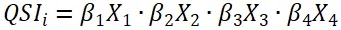
       3  指数

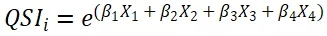
       其中，β表示旅客对相应要素的偏好权重（preference weight）。得到同航线市场不同行程的“打分”QSI之后，我们可以估计旅客选择不同行程的概率，或者说是该行程在其市场的份额：

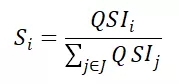
       其中，

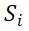      表示行程i的市场份额；

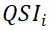     表示行程i的服务质量指数；

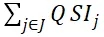     表示和行程i分享同一个航线市场的行程的服务质量指数之和。

       对于具体的某家航空公司而言，它在一个航线市场中承运的所有行程的市场份额的总和，就是它在这个市场的份额。

       在训练模型时，我们通常有两种方法来确定QSI模型中β的值：

       ① 根据经验或业内专家的建议设定；

       ② 基于历史数据，使用统计学或是机器学习的方法对β进行参数估计。

       优缺点

       QSI模型非常容易理解，粗略来讲，就是给每个行程“打分”，依据“分数”QSI，把份额按比例分配给每个行程。但QSI模型也有两个明显的缺点：

       · 偏好权重的设定相互独立

       不论是由专家直接给定，还是利用历史数据进行参数估计，不同要素X的偏好权重β的获取是相互独立的。换句话说，QSI模型不能反映不同要素之间的相关性。例如，直飞航班（途径中间站点数为0）所需的飞行时长通常小于联程航班所需的飞行时长（途径中间站点数大于等于1）。

       · 弹性问题（the elasticity problem）

       受不同行程间相关性影响，行程i的改变对同市场中其他行程的影响应该是有所差异的，但QSI模型认为这种影响是相同的。理论上，我们也可以通过计算行程i的QSI变化所引起的行程j市场份额变化的交叉弹性方程（cross-elasticity equation）来体会：

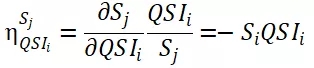
       等式右边修订为-Si，是关于i的表达式，也就是说，行程i的QSI变化所引起的行程j的市场份额变化只与i有关，与j无关。这显然是不合理的。例如，i作为上午的行程，当它降低票价，导致了QSIi的变化，则会对临近时间的行程有较大影响（旅客都跑去选i了），对下午以及晚上的行程影响较小。

      03  MNL模型

      历史

      各个行程的市场份额深受旅客的选择行为影响，因此航空业经常用离散选择模型来预测市场份额。Mcfadden于1973年最早提出了Logit离散选择模型，基于效用最大化理论对个体的选择行为进行模拟。通过多年的研究应用发展出了二项式Logit（Binary Logit）、多项式Logit（MNL）、嵌套Logit（Nested Logit）等模型。其中，MNL模型是出行行为研究领域应用最广泛最成熟的方法之一。Coldren 等人第一次采用MNL模型来预测航线市场各个行程的市场份额，他们考虑了产品服务评分、路径衔接质量、航空公司市场占有率、机票价格、机型等影响因素。

       模型

       MNL旨在通过效用函数，分析个体对于不同行程的选择概率，进而估算市场份额。其行为理论基础是随机效用理论，该理论认为人们在做决策时都是按照效用最大化的原则进行。一般情况下，MNL的效用函数和QSI模型的线性表现形式相似，为：

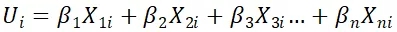
       其中，

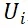       某航线可选行程i的效用值；

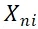       行程i的要素n的观测值；

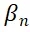       和要素n相关的参数。

       考虑到不可观测的误差部分，效用函数也可以被表示为：

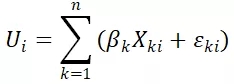
       其中，

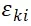       表示误差部分。

       由此，从旅客n的某航线备选行程集合中的j个备选行程中选择行程i的MNL概率，可以被表示为：

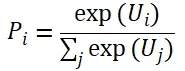
       其中，

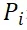       表示行程i的市场份额；

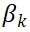       估计方法和QSI相似，在实际应用中，MNL的参数估计通常会采用最大化对数似然估计法。

       优缺点

       由于结构简单、稳定性高，MNL模型在离散选择模型中是最为常用的。同时它的限制性也较强，体现在：

       · 缺乏随机性

       估算出的参数β只能代表旅客偏好的平均水平。

       · 不相关选择的独立性（IIA）

       同市场中，选择行程i的概率Pi和选择j的概率Pj的比率与其它该市场中的任何行程z的Uz变化无关。该性质和QSI的弹性问题相似，同样可以通过观察行程i要素值变化引起行程j概率变化的交叉弹性方程来得到：

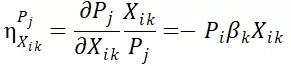
       在这个式子中，最右边的表达式与j无关，体现了交叉弹性在不同行程方案之间没有差别，这意味着一个行程效用的改善将从所有其他替代行程方案中按相同比例获得市场份额。这显然不符合实际。

       除了航线的决策和评估，在考虑重捕获率的航网优化建模和基于旅客选择的收益管理中，它同样发挥着重要的作用。

       04  基于算例的模型比较和应用

       可以看到，不论是QSI模型，还是MNL模型，我们在使用它们来估计市场份额的时候，都需要以下步骤：

       01 特征提取：确定X，提取影响旅客选择行程的要素；

       02 参数估计：对模型中β进行参数估计；

       03 预测份额：利用训练得到的模型预测市场份额。

       模型效果对比

       QSI模型和MNL模型都是被广泛应用的估计航空公司市场份额的模型，我们到底怎么选择好呢？

       Coldren等人的实验结果显示，MNL预测总是优于QSI模型，其预测误差相对于QSI减少了10-15%，而且预测结果相对稳定。然而，Jacobs等人曾在《Quantitative Problem Solving Methods in the Airline Industry》一书中提到，根据他们对行业专家的采访，使用MNL等方法的航空公司考虑重新使用QSI模型，因为航司觉得MNL等模型很复杂，参数估计很麻烦。对比Jacobs等人解释称，使用效果和预想的有差异并不是MNL的问题，而在于采用了过度参数化的效用函数。此外，虽然QSI模型和MNL模型都存在不能反映行程之间动态的相互影响的问题，但是Garrow提到可以通过MNL的拓展模型来松弛IIA这个假设。

       杭州UMAX算法团队利用国内的民航数据进行了MNL和QSI的对比实验。综合考虑了：航线区域（华北、华中、华东、华南、东北、西北、西南）、航线性质（商务线、旅游线、混合线）、航线密度（日均航班数）、竞争程度（承运人数量）、航线距离和航线盈利能力（客座率、客公里收入）等因素。以尽可能包含各类航线为目标，筛选出了12条航线，以它们一个月的数据来进行模型训练与效果评估，力求使结果更具有说服力。

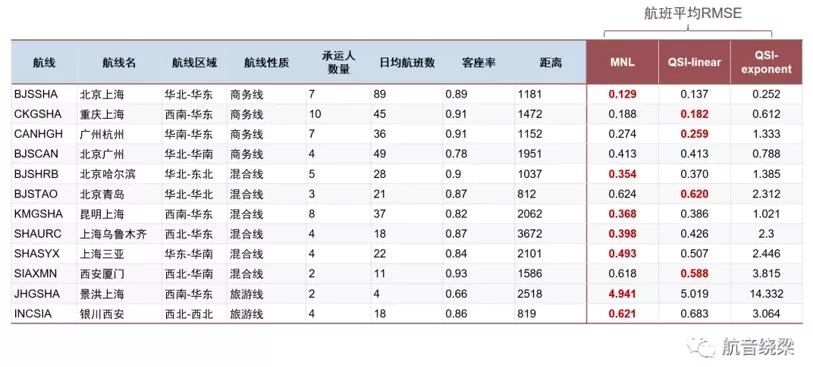
UMAX实验结果：MNL模型基本上优于QSI模型的结果

       为了测试模型的泛化误差，团队使用了交叉验证留一法（Leave-One-Out Cross Validation）对两个模型的效果进行评估，即将某航线整月的数据集按日分为30组，每次只留某航线一天的数据作为测试集，剩下的作为训练集。并选择RMSE均方根误差作为评估指标，取多次验证得到的评估指标均值作为最终评估结果。结果表明：①MNL模型的训练效率更高：初始值依赖小，收敛更快；②MNL有7条航线预测更准确，预测效果总体上优于QSI。

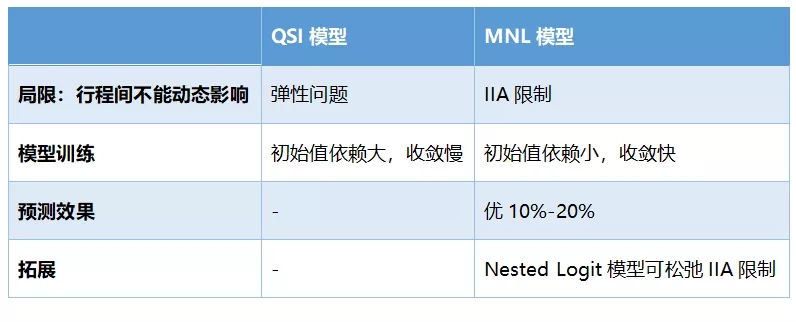
       应用实例

       由前一节可知，MNL模型效果相对更好。因此团队基于训练得到的MNL模型对厦门西安航线进行了两种场景下的市场份额预测：

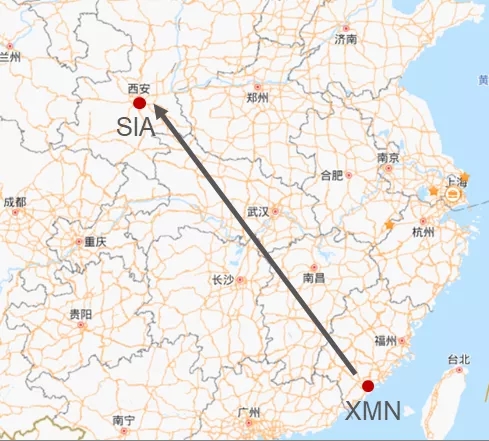
       原来的航线市场份额分布如下:

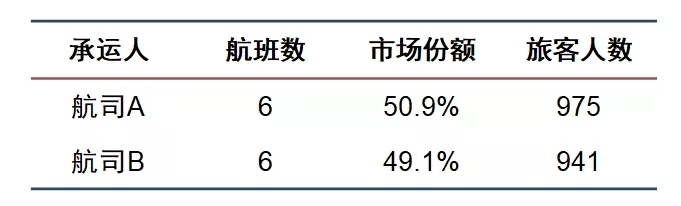
       该航线市场主要由两家航司运营，且份额相似。

       · 场景一：增加频次

       新增航班信息：

       使用MNL模型进行预测，结果如下：

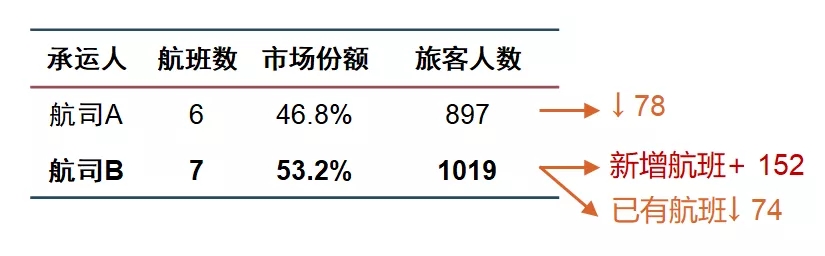
       基于这个结果，航司B便可以评估通过新增该航班来扩大自己的市场份额是否值得。在已经确定要新增该航线航班的情况下，同样可以通过MNL模型来判断不同的时刻价值和飞机容量价值，帮助决策。

       · 场景二：航司开辟新航线

       新增航班信息：

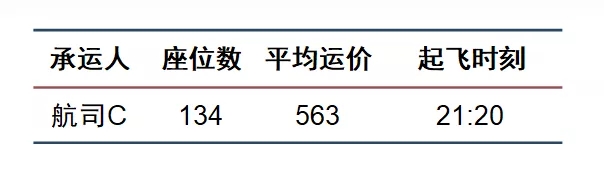
       结果：

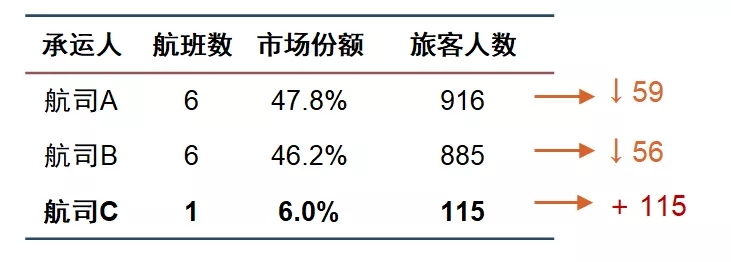
       可见，新航司的航班投放会一定程度降低现有航司的市场份额。通过MNL模型，可以帮助航司评估开辟一条新航线的必要性。

参考：

[1] Kloth R J, et al. Method and apparatus for implementing a quality of service policy in a data communications network: US, US6870812[P]. 2005.

[2] Barnhart C, Smith B (2012). Quantitative Problem Solving Methods in the Airline Industry: A Modeling Methodology Handbook. Boston, MA: Springer.

[3] Coldren G M, Koppelman F S, Kasturirangan K, Mukherjee A (2003). Modeling aggregate airtravel itinerary shares: logit model development at a major U.S. airline. Journal of Air Transport Management 9(6):361–369.

[4] Garrow LA (2010) Discrete choice modelling and air travel demand: theory and applications. Ashgate, Aldershot.

[5] Mcfadden D. Conditional Logit Analysis of Qualitative Choice Behavior[J]. Frontiers in Econometrics, 1974:105-142.