航线网络规划(四):拓展与应用
从夏末到深秋,时光匆匆,我们的航线网络规划系列也接近尾声。在之前的三期推文中,我们为大家介绍了航网问题的关键要素,包括航线频率、航班时刻、市场份额估计、机型分配等。新关注的小伙伴可以点击回顾:
本期推文,作为收官,我们将讨论一些基于机型分配问题的拓展考量:(1)旅客的溢出与重新捕获,(2)航班计划的一致性,(3)计划的鲁棒性,(4)机组资源限制,(5)机务资源限制,(6)受分配座位数影响的票价。
01 旅客的溢出与重新捕获
在求解基于行程的机型分配模型时,我们发现有限的飞机资源和错综复杂的航线网络仍会导致部分旅客需求无法被满足,该现象被称之为“旅客溢出”。
举个小例子:预测得到某航班的旅客需求为150人,而航空公司只能提供座位数为100的飞机,那么就存在50名潜在旅客无票可买。

图源:网络
在实际生活中,溢出的旅客会有更进一步的决策。作为一名旅客,当心仪航班余票为0时,他可能会选择起终点与原计划一致的替代航班、其它交通方式或者不得不取消旅行。
以刚才的50名溢出乘客为例,可能会存在30名旅客选择其它航班,15名旅客乘坐高铁出行,剩下的5名旅客取消旅行的情况。从航空公司的角度看,这30名选择其它航班的乘客有再次成为自己客户的可能。这类情况被称为“旅客重捕获”。
旅客重捕获的建模,可以通过在航线网络规划(三):机型分配问题给出的基于行程的机型分配模型的基础上,引入“重捕获率”实现,其表示行程p溢出的旅客被行程r重新捕获的概率,可以利用航线网络规划(二):航线评估与决策提到的QSI指数计算,如下所示。
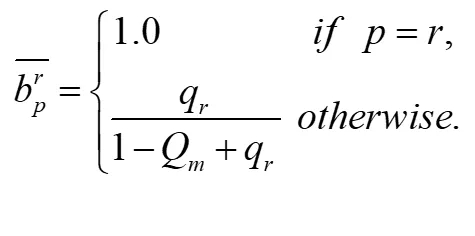
Qm表示航司在行程p所属的航线市场m内的所有行程的QSI指数(q表示)之和,可以理解为该航司在这个航线市场的占有率,(1-Qm)就表示其他航司的占有率。也就是说,对于该航司来说,自己的旅客溢出时,想要重捕获这部分旅客必须和其它航司在该航线的行程进行竞争。
最后,我们可以把求得的旅客重捕获率结合溢出旅客的重分配变量融入模型中进行求解,从而提供一个切实可行的分配方案。
02 航班计划的一致性
我国的航空公司的航班计划一般以周为单位编排,即每周一循环。具体的表现为,有的航班每天都执行,有的航班隔天执行,有的航班只在一周的固定某几天执行。
考虑到时刻资源宝贵,且部分航线的需求并没有那么旺盛,或者不是每天都有充足的需求。例如,商务航线的旅客集中在周内、旅游航线的旅客可能集中在周末。因此某些航线不会每天都排航班,而是把需求引导到集中的某几天。如此一来,同样的时刻就可以被多个航线充分利用。
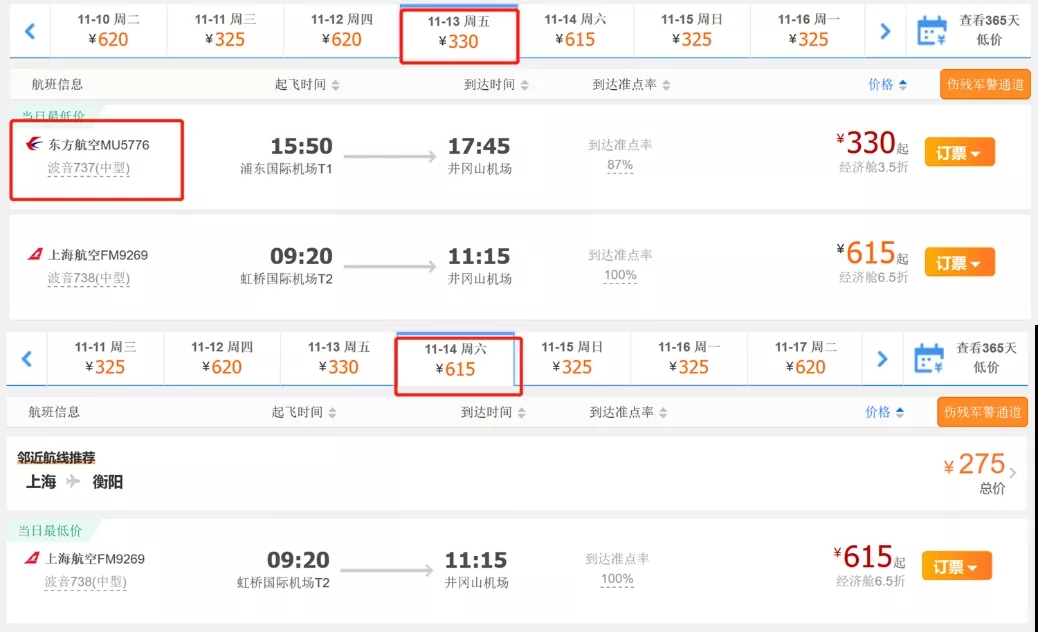
MU5776只在周一、三、五、日执行,图源:携程
虽然一周内不是每天的航班表都完全相同,但是对于同一个航班还是需要遵循一些“一致性”原则,为运营提供便利,节约成本,提高服务水平。首先,对于经常出差的商务旅客,会希望自己常坐航班的起降时刻总保持一致,因为航班时刻经常变更可能会给他们的出差计划造成不便。因此,我们需要在做航班计划时注意考虑时刻同步约束(Synchronization Constraints),为每个航班在一周内的不同星期安排相同的起降时刻。这样的航班计划表可以帮助提高飞机计划的可靠性,在实际执行阶段的可维护性高,也能节省开支。
类似地,商务旅客也更习惯自己熟悉的航班总是安排相同的机型,经常坐的宽体机被换了窄体机、或者机型大小总是变来变去,都会降低商务旅客的满意度。所以我们在为航班安排机型的时候需要考虑机型一致性约束(Homogeneity Constraints),使得每个航班每次能被安排到相同的机型。这样的航班计划表也会使地面服务的安排变得更加容易。
03 计划的鲁棒性
实际执行计划时,不可预测的事件(如恶劣天气、空中交通管制等)时有发生,航班可能无法按计划如期起飞或抵达。为了缓解突发事件带来的恶劣影响,我们有许多提高计划鲁棒性的方法。最为常见的手段是最小化计划的期望延误,此外,我们还可以通过增强计划的某些“特征”,来帮助提高计划的鲁棒性,例如:
同一架飞机应尽可能在单一基地和其他非基地机场间往返,减少多个基地机场间的耦合性。换句话说,就是围绕飞机的属地机场,重复“出去-回来”。这样的飞行计划在实际执行阶段可以提供更多的航班取消机会,也就是每次取消一对“往返”。
机场纯度(Station Purity)也可以用来衡量计划的鲁棒性。给定机场,机场纯度表示为该机场服务的机型的数量。通过限制每个机场的机场纯度,可以为飞机以及机组人员提供更多的交换航班的机会,从而提高计划的鲁棒性。
04 机组资源限制
出于安全的考虑,机组排班需要满足十分复杂的约束。同时,在编排机组人员飞行计划时,也需要考虑飞行员的可行性和经济性。此外,随着我国飞行员的紧缺程度增加,航空公司不仅希望从运营层面优化机组排班:利用可用机组资源尽可能地满足商委制定的飞行任务;也希望从宏观层面把控机组资源的分配。
更具体的来说,根据民航局的规定(R6),一个飞行员全年飞行小时不超过900,每月飞行小时不超过100。显然100×12>900,这也意味着飞行员的飞行小时在各个月份的分配是有一定波动的。那么,给哪几个月分配较多的飞行小时,给哪几个月分配较少的飞行小时,是需要根据市场波动慎重决策的。
在实践中,由于缺乏相关的科学方法,机组管理中心通常将全年的飞行小时平均分配到各个月份,假设每个月飞行平均飞行900/12=75个小时,再根据往年市场行情、休假分布等进行微调。商委会协调机组管理中心给出的每月可用飞行小时数,安排航班任务量。然而,上述分配方式显然有很大的改进空间。具体而言,国内市场的旺季一般分布在暑运和春节,国庆、圣诞元旦等节假日也会带来相当的需求增长,而其他月份为淡季市场。
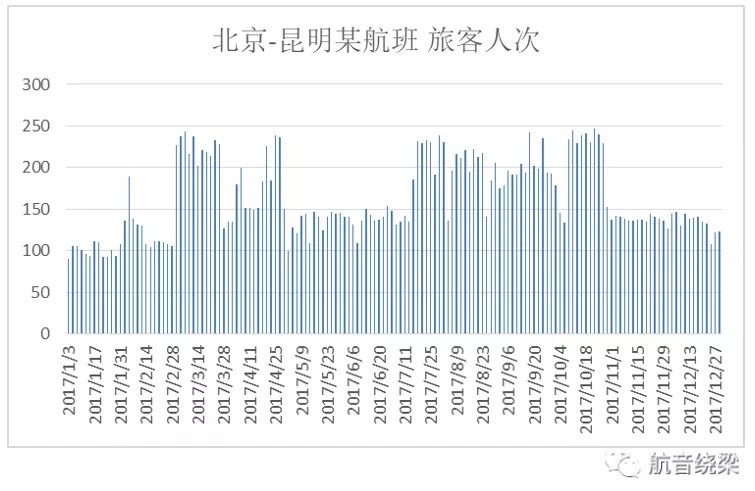
可以想见,航空市场在各个月份的需求波动是比较大的,如果均匀地分配飞行小时,势必会导致大量的旺季需求由于机组资源的匮乏而不能被捕捉到。特别是年末的旺季,经常由于飞行小时不够而放弃大量高价值的航班。极端情况下,有可能年初淡季虚耗的一个飞行小时,放在年末可以带来几十倍甚至百倍的创收。因此,如何贴合市场的波动,合理分配飞行小时是一个值得深入研究的问题。课题组也这在进行相关研究,希望通过将机型分配问题和机组资源分配问题整合考虑,来解决此问题。
图片
图源:网络
05 机务资源对机型分配的限制
为了保证飞机的适航性,飞机需要定期进行维护,包括航前、航后维护等灵活性较高的维护,以及C检、D检等相对固定的维护。而这些维护作业的顺利进行,离不开良好的机务资源分配,即合理安排飞机在什么时段在哪个航站进行哪些维护。传统上,机务管理中心会根据商委给出的机型分配结果,安排每架飞机的飞行路径和维护计划。然而,随着飞机数量的增多,这样的工作方式经常给维护计划的制定带来了很大的困难。因此,航空公司希望能在机型分配时,考虑机务资源的限制。
通常,对于有计划的大修,商委会与机务管理中心沟通,减少相应机型的任务量,相当于在维护时间段减少一架飞机,相对容易处理。但是大修前后航班的衔接,以及相对频繁的维护任务,商委很难考虑到。一种比较直接的处理方法是,将机型分配与飞机路径以及维护计划一起考虑,但这样的整合问题通常规模较大不易求解,且很难考虑到一些细节约束。因此,课题组也在进行相关研究,希望研发出具备操作性的算法。
06 受分配座位数影响的票价
在为航班安排机型时,我们常常要用到航班的需求和票价。最容易想到的评估方法是参考历史数据的平均需求和平均票价,也就是取历史数据的均值。
这种“一刀切”的粗略方法对于以京沪线为代表的精品商务航线是适用的。某航司2017年历史数据显示,不论安排哪一种机型,京沪线的票价总是能维持相对的高位稳定。
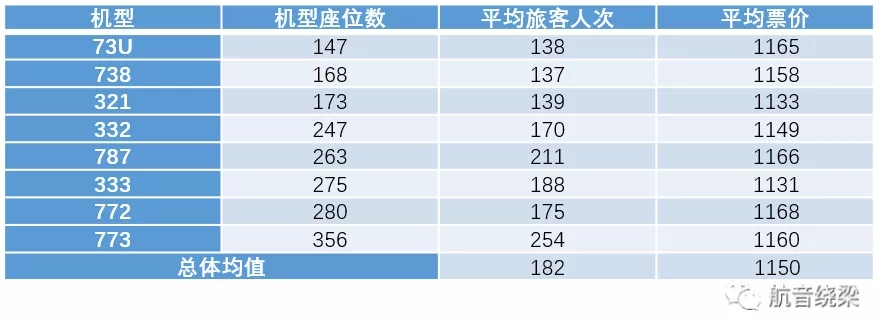
但是对于其他航线,例如杭州-深圳,通过统计观察具体的历史数据,不难发现:当分配的座位数增加时,一方面旅客人数有所上升,另一方面平均票价却降低了。
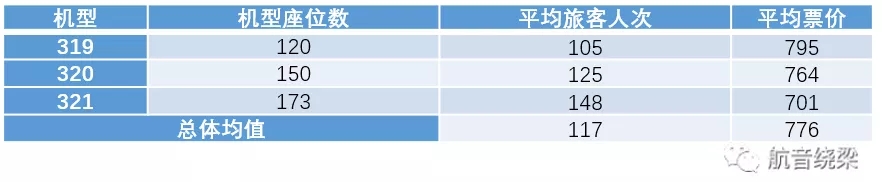
我们可以简单地理解为,当把机型从空客319换成320时,虽然多提供了30个座位并获得了20位旅客,但是这20位旅客的“价值”不如之前的105位旅客的高,所以平均票价就降低了。值得注意的是,这20位旅客的平均票价不是764,而是更低的(764×125-795×105)/20=601。
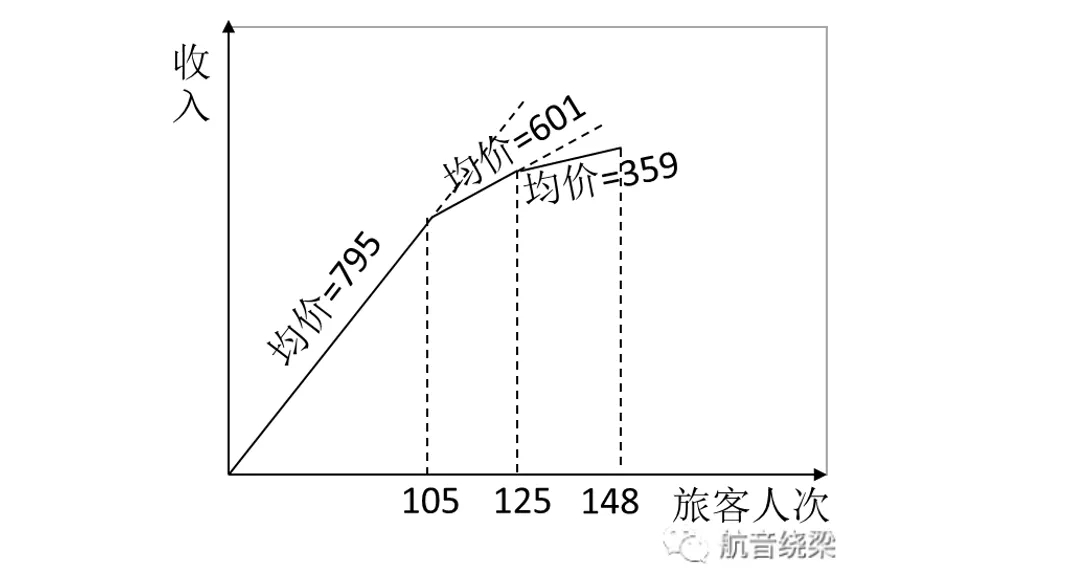
显然,我们需要考虑,这20位旅客是否值得我们付出更多成本来提供更多座位;有可能,我们把这些座位数留给其他航线才是更好的选择。准确决策需要我们更细致地刻画“分配座位数-票价”的关系。
考虑到航班的票价会受到分配座位数影响,粗略地使用固定的历史平均需求和历史平均票价并非总是合理的(除非价格像京沪线那么稳定)。为此,课题组正在开展相关的研究,希望能充分挖掘航班历史数据中的信息价值,帮助航司更精准地为航班分配机型。更进一步地,此项研究或许也有助于我们更加科学地决策:付出额外的成本改造部分飞机的内部布局,增加更多的座位数,是否能产生足够的经济效益。
- END-
参考文献:
[1] Barnhart, C., Boland, N.L., Clarke, L.W., Johnson, E.L., Nemhauser, G.L., Shenoi, R.G., 1998. Flight string models for aircraft fleeting and routing. Transportation Science 32, 208–220.
[2] Barnhart C , Knoker T S , Lohatepanont M . Itinerary-based airline fleet assignment[J]. Transportation ence, 2002, 36(2):199-217.
[3] Bélanger N, Desaulniers G, Soumis F, et al. Weekly airline fleet assignment with homogeneity[J]. Transportation Research Part B: Methodological, 2006, 40(4): 306-318.
[4] Gao C, Johnson E, Smith B (2009). Integrated airline fleet and crew robust planning. Transportation Science, 43(1): 2–16.
[5] Ioachim I, Desrosiers J, Soumis F, et al. Fleet assignment and routing with schedule synchronization constraints[J]. European Journal of Operational Research, 1999, 119(1): 75-90.
[6] Klabjan D, Johnson E L, Nemhauser G L, Gelman E, Ramaswamy S (2002). Airline crew scheduling with time windows and plane-count constraints. Transportation Science, 36(3): 337–348.
[7] Liang, Z. and Chaovalitwongse, W.A. (2012), “A network-based model for the integrated weekly aircraft maintenance routing and fleet assignment problem”, Transportation Science, Vol. 47 No. 4, pp. 493-507.
[8] Lohatepanont, M., Barnhart, C., 2004. Airline schedule planning: Integrated models and algorithms for schedule design and fleet assignment. Transportation Science 38, 19–32.
[9] Rosenberger J M, Johnson E L, Nemhauser G L. A robust fleet-assignment model with hub isolation and short cycles[J]. Transportation science, 2004, 38(3): 357-368.
[10] Smith B C, Johnson E L. Robust airline fleet assignment: Imposing station purity using station decomposition[J]. Transportation Science, 2006, 40(4): 497-516.



